Belleza en matemáticas
Objetivos
De lo imposible a lo evidente
- Asombro → “¿Cómo puede ser cierto?”
- Método → Aplicamos reglas simples y lógica.
- Claridad → Lo que parecía magia se vuelve obvio.
- Belleza → Descubrimos el placer de comprender.
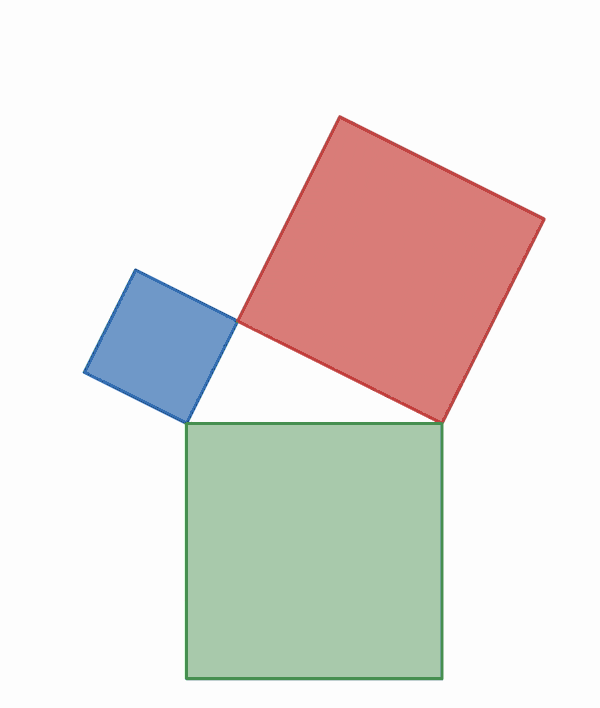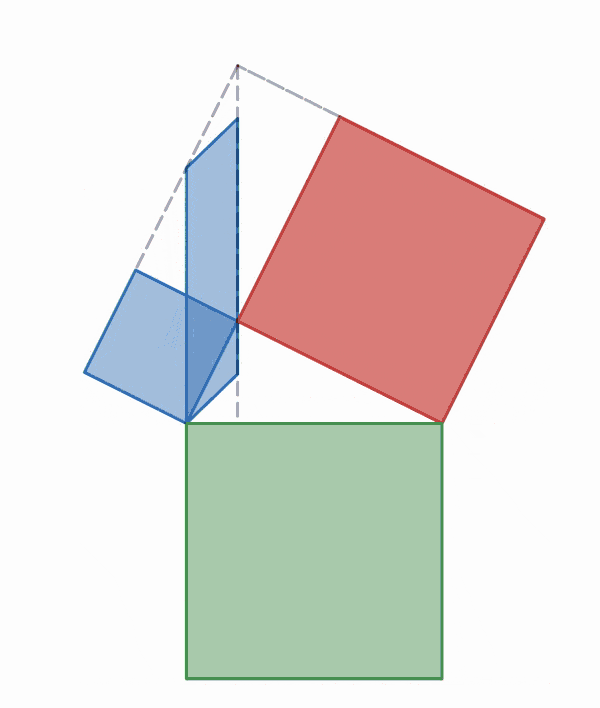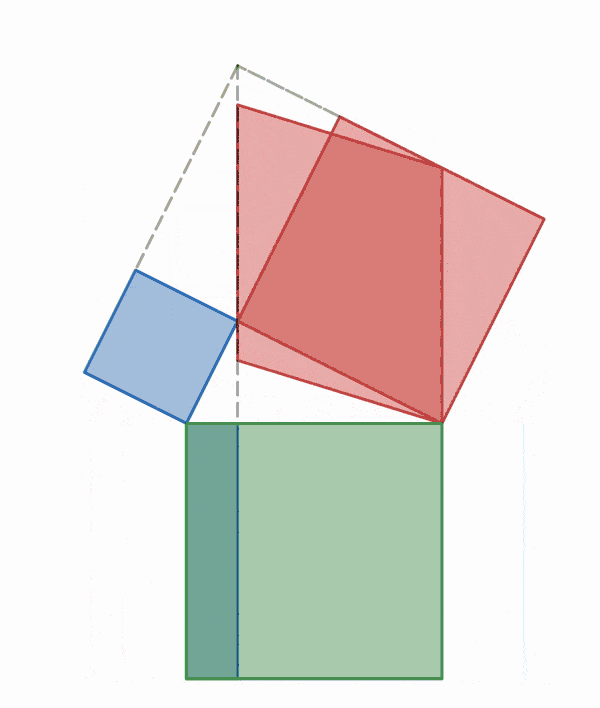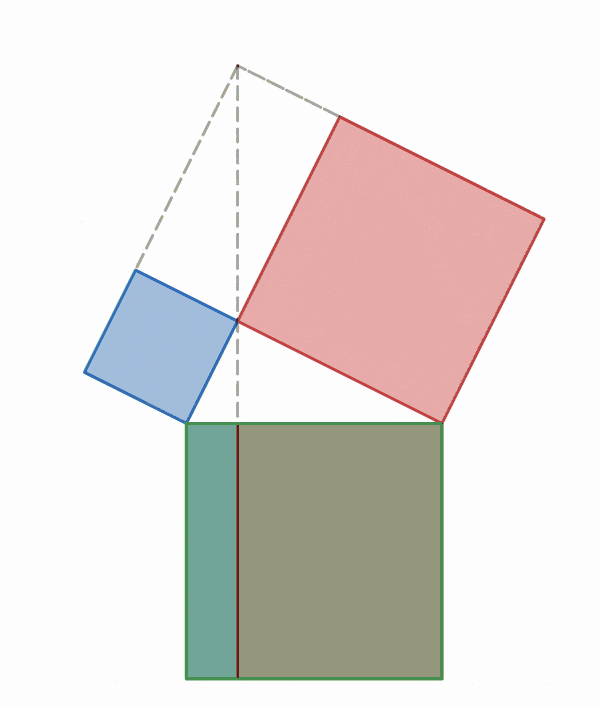
Suma de Gauss
Problema: \[
1 + 2 + 3 + \cdots + 100
\]
Escribe la suma dos vecesde la forma: \[ S = 001+ 002+\cdots+099+100 \] \[ S = 100+099+\cdots+002+001 \]
\(\Rightarrow 2S = 101 + 101 + \cdots +101\)
\(\Rightarrow 2S = 100(101)\)
\[ \displaystyle S = \frac{100(101)}{2} = 5050\]
Suma de Gauss
¿ números impares y los cuadrados?
¿ números impares y los cuadrados?
\[ 1 + 3 + 5 + \dots + (2n-1) = n^2 \]
- Ejemplos: \(1=1\), \(1+3=4\), \(1+3+5=9\), …
- Para \(n\) se cumple, …. se cumplirá para \(n+1\)?
\[ 1 + 3 + 5 + \cdots + (2n-1) + (2n+1) \]
\[ = n^2 + (2n+1) \]
\[ = n^2 + 2n + 1 \]
\[ = (n+1)^2 \]
Qué son las Olimpiadas
- Competencias de ingenio y creatividad.
- Problemas simples en apariencia, profundos en ideas.
- A nivel local, nacional e internacional (IMO).
- Inició en 1959 en Rumanía (7 países).
- Hoy reúne a más de 100 países.
- Competencia más prestigiosa en el mundo.
- Inició en 1959 en Rumanía (7 países).
El profesor Pawel Kröger de la USM fue medallista en la IMO: oro en 1972 y plata en 1973.
Ejemplos de Olimpiadas
Trayectorias albas en un tablero 8×8
En un tablero de ajedrez 8×8 (32 casillas blancas y 32 negras) llamaremos trayectoria alba a una secuencia de 8 casillas blancas, una por fila, de modo que casillas consecutivas se toquen en un vértice (es decir, pasan de una fila a la siguiente en diagonal).
- Ejemplo:
- la diagonal de casillas blancas es una trayectoria alba.
Determine cuántas trayectorias albas hay en total.
Trayectorias albas en un tablero 8×8
Trayectorias albas en un tablero 8×8
El problema pide poner una ficha en cada fila, tocando siempre a la de arriba en un vértice.
Esto es como un rey de ajedrez que empieza en la fila 1 y baja hasta la fila 8, moviéndose solo en diagonal (↙ o ↘) por casillas blancas.
Para contar los caminos posibles usamos programación dinámica, sumando paso a paso cuántas formas hay de llegar a cada casilla.
✅ Solución: 296 trayectorias albas
Pirámide de Naranjas
Se tienen 680 naranjas apiladas en una pirámide triangular. ¿Cuántas naranjas hay en la base de la pirámide?
Hints
- Una pirámide triangular se forma apilando triángulos: el nivel de abajo tiene \(n\) naranjas por lado, el siguiente \(n-1\), y así hasta llegar a la punta.
- La suma de los primeros \(n\) números es:
\[ 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2} \]
- La suma de los primeros \(n\) cuadrados es:
\[ 1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6} \]
Pirámide de Naranjas
En la base hay un triángulo de lado \(n\) con \(\displaystyle \frac{n(n+1)}{2}\) naranjas.
Una pirámide triangular es la suma de todos esos triángulos desde \(1\) hasta \(n\). Eso equivale a: \[ \sum_{i=1}^n \frac{i(i+1)}{2} = \frac{1}{2} \sum_{i=1}^n (i+i^2) = \frac{n(n+1)(n+2)}{6} \]
Planteamos la ecuación:
\[ \frac{n(n+1)(n+2)}{6} = 680 \rightarrow n = 15 \]
Entonces, en la base hay: \(\displaystyle \frac{15 \times 16}{2} = 120\) naranjas.
Misterios de las matemáticas
- Aún hay preguntas sin respuesta en matemáticas.
- Son tan difíciles que llevan décadas esperando solución.
- Algunos ejemplos:
- Hipótesis de Riemann → sobre los números primos
- Navier–Stokes → cómo se mueven los fluidos
- Conjetura de Hodge → formas en geometría
- Conjetura de Poincaré → formas de los espacios en 3D
- Hipótesis de Riemann → sobre los números primos
✅ La Conjetura de Poincaré fue resuelta en 2003 por el matemático ruso Grigori Perelman.
Conceptos Claves
Conjetura
Afirmación que parece cierta, falta demostrar.
Ej: Goldbach (todo par > 2 es suma de dos primos)
Hipótesis
Suposición precisa pero sin prueba.
Ej: Hipótesis de Riemann (sobre los números primos)
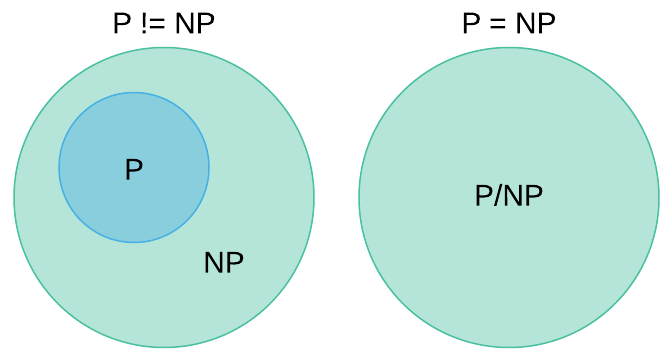
Problema abierto
Gran pregunta sin respuesta aún.
Ej: P vs NP (resolver rápido = verificar rápido?)
¿Cómo nos apoya la computación?
- Analiza masivamente muchos casos en poco tiempo.
- Detecta patrones en tablas, gráficos y relaciones.
- Encuentra contraejemplos con facilidad.
- Prototipa ideas: del código a la evidencia en minutos.
Veamos ejemplos en problemas abiertos (y casi abiertos).
Aprendizajes
La matemática es arte
Cada demostración descubre la belleza escondida en los números.
Olimpiadas de matemáticas
Despiertan ingenio y fortalecen el razonamiento creativo.
Problemas Abiertos
Las matemáticas guardan misterios sin resolver.
Disfrutar el proceso
Explorar, equivocarse y asombrarse es parte de aprender a pensar.
¡Que Comiencen los Juegos!
